POHON (LANJUTAN)

POHON (Lanjutan)

A.Pohon Berakar (rooted tree)

Pohon berakar yang urutan anak-anaknya penting disebut pohon  terurut (ordered tree).

1.Anak (child atau children) dan Orangtua (parent)

b, c, dan d adalah anak-anak simpul a,  a adalah orangtua dari anak-anak itu a.

2. Lintasan (path)

Lintasan dari a ke j adalah a, b, e, j.  Panjang lintasan dari a ke j adalah 3.

3. Saudara kandung (sibling)

f adalah saudara kandung e, tetapi g bukan

saudara kandung e, karena orangtua mereka  berbeda.

4. Upapohon (subtree)

5. Derajat (degree)

Derajat sebuah simpul   adalah   jumlah  upapohon           (atau     jumlah  anak) pada simpul tersebut.

Derajat a adalah 3, derajat b adalah 2,  Derajat d adalah satu dan derajat c adalah 0.

Jadi, derajat yang dimaksudkan di sini adalah derajat-keluar.

Derajat maksimum dari semua simpul merupakan derajat pohon itu  sendiri. Pohon di atas berderajat 3

6. Daun (leaf)

Simpul yang berderajat nol (atau tidak mempunyai anak) disebut

daun. Simpul h, i, j, f, c, l, dan m adalah daun.

7. Simpul Dalam (internal nodes)

Simpul yang mempunyai anak disebut simpul dalam. Simpul b, d,e, g, dan k adalah simpul dalam.

8. Aras (level) atau Tingkat

9. Tinggi (height) atau Kedalaman (depth)

Aras maksimum dari suatu pohon disebut tinggi atau kedalaman

pohon tersebut. Pohon di atas mempunyai tinggi 4.

B.Pohon Terurut (ordered tree)

Pohon berakar yang urutan anak-anaknya penting disebut pohon  terurut (ordered tree).

C.Pohon n-ary

• Pohon   berakar yang      setiap    simpul  cabangnya           mempunyai  paling banyak n buah anak disebut pohon n-ary.
  

< sentence>

• Pohon n-ary dikatakan teratur atau penuh (full) jika setiap  simpul cabangnya mempunyai tepat n anak.

D.Pohon Biner (binary tree)

~        Adalah pohon n-ary dengan n = 2.

~        Pohon yang paling penting karena banyak aplikasinya.

~        Setiap simpul di adlam pohon biner mempunyai paling  banyak 2 buah anak.

~        Dibedakan antara anak kiri (left child) dan anak kanan  (right child)

~        Karena ada perbedaan urutan anak, maka pohon biner  adalah pohon terurut.

 

E.Pohon Biner Seimbang

Pada beberapa aplikasi, diinginkan tinggi upapohon kiri dan tinggi  upapohon kanan yang seimbang, yaitu berbeda maksimal 1.

F.Terapan Pohon Biner

1. Pohon Ekspresi

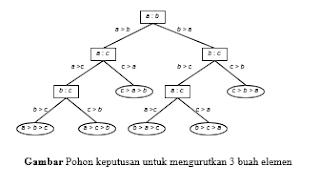
2. Pohon Keputusan

3. Kode Awalan

4. Kode Huffman

graf(pohon)

MATEMATIKA DISTRIT

=POHON=

1.      Defenisi

Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit .

2.      Sifat-sifat pohon 

3.       

Pohon Merentang

Pohon merentang di perole dengan memutus sirkuit di dalam graf.

           

Setiap graf terhubung mempunyai paling sedikit  satu buah ppohon merentang.

Graf tak-terhubung dengan k komponen mempunyai k buah  hutan merentang yang disebut hutan merentang (spanning  forest).

4.      Aplikasi pohon merentang

1.Jumlah ruas jalan seminimum mungkin  yang  menghubungkan semua kota sehingga setiap kota tetap  terhubung  satu sama lain.

2.Perutean (routing) pesan pada jaringan komputer.

             Pohon merentang minimum

Graf terhubung-berbobot mungkin mempunyai lebih dari 1  pohon merentang.

Pohon merentang yang berbobot minimum –dinamakan pohon  merentang minimum (minimum spanning tree)

5.      Algoritma Prim

Langkah1 : ambil sisi dari graf           G yang berbobot minimum,masukkan ke dalam T.

Langkah 2 : pilih sisi (u, v) yang mempunyai bobot minimum dan  bersisian dengan    simpul di T, tetapi (u, v) tidak  membentuk sirkuit di T. Masukkan (u, v) ke dalam T.

Langkah 3 :ulangi langkah 2 sebanyak n – 2 kali.

Contoh :